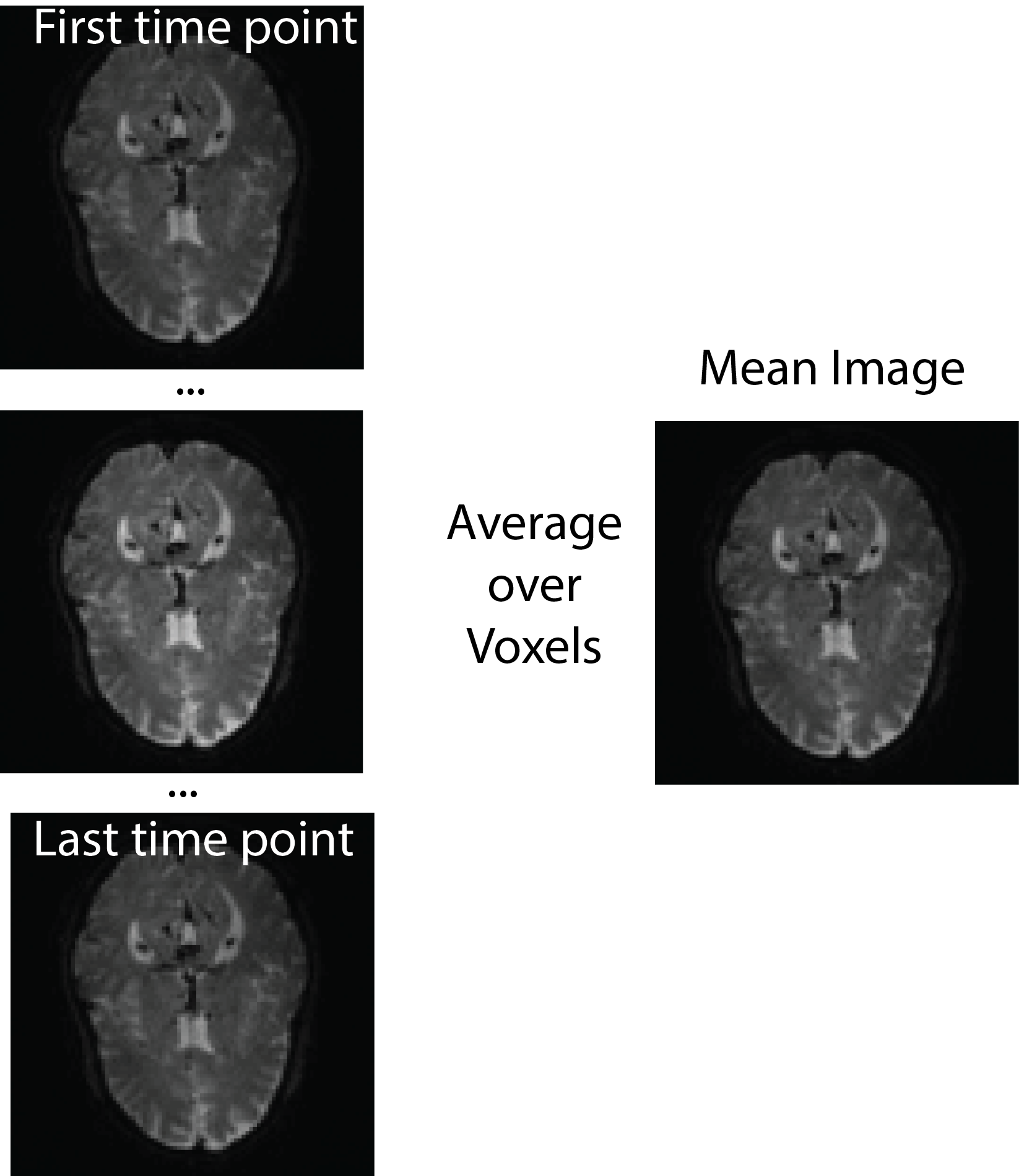
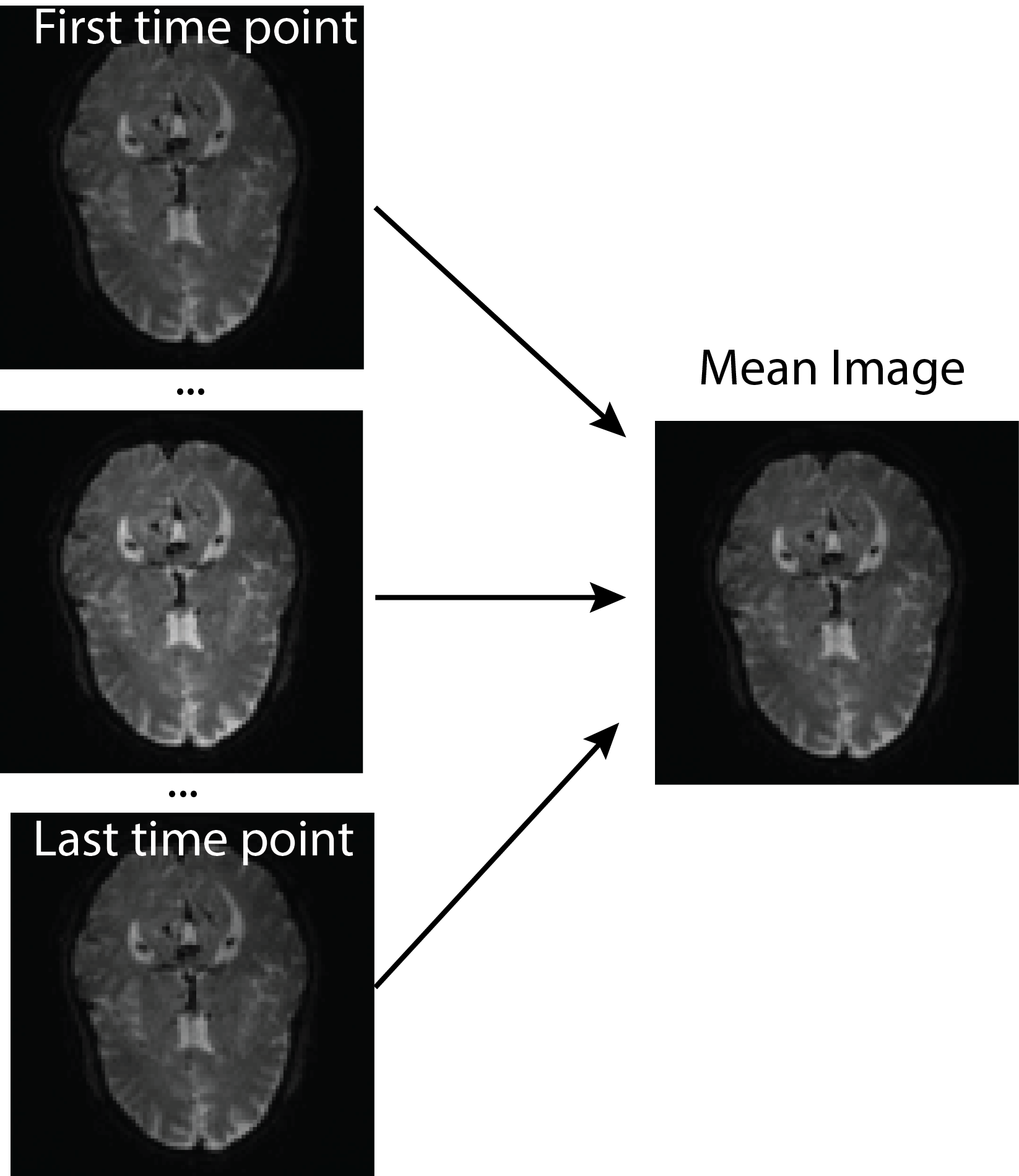
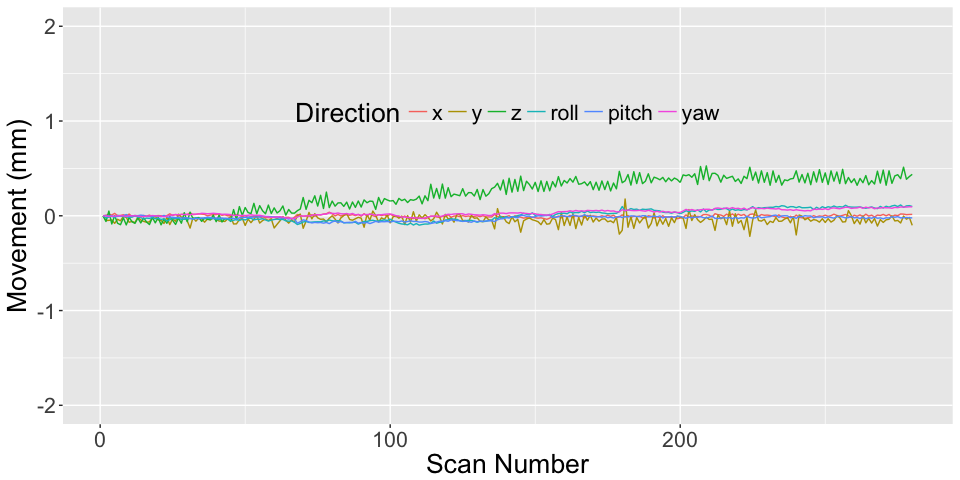
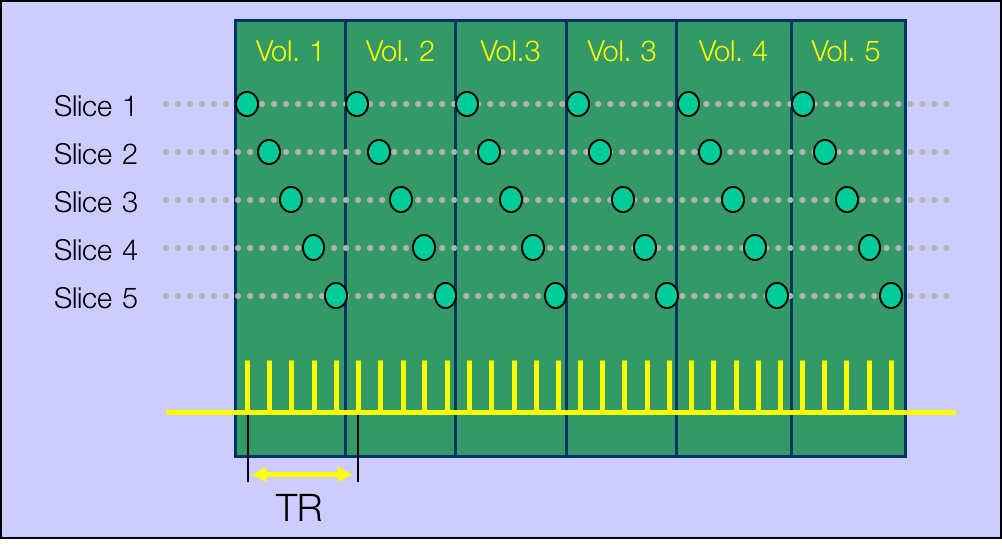
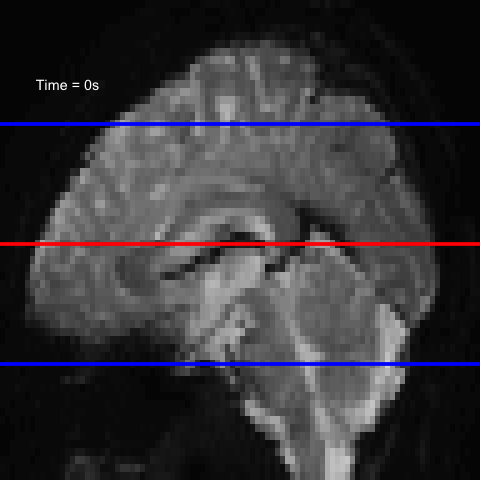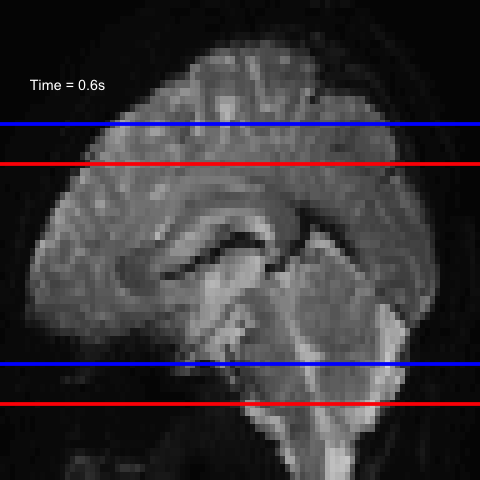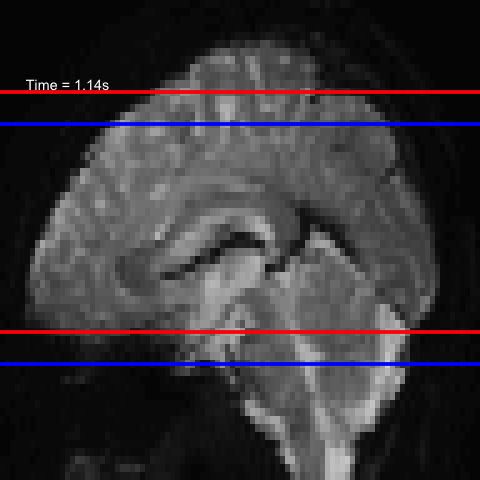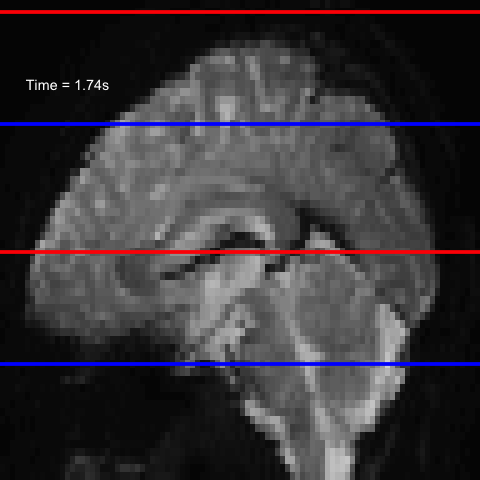
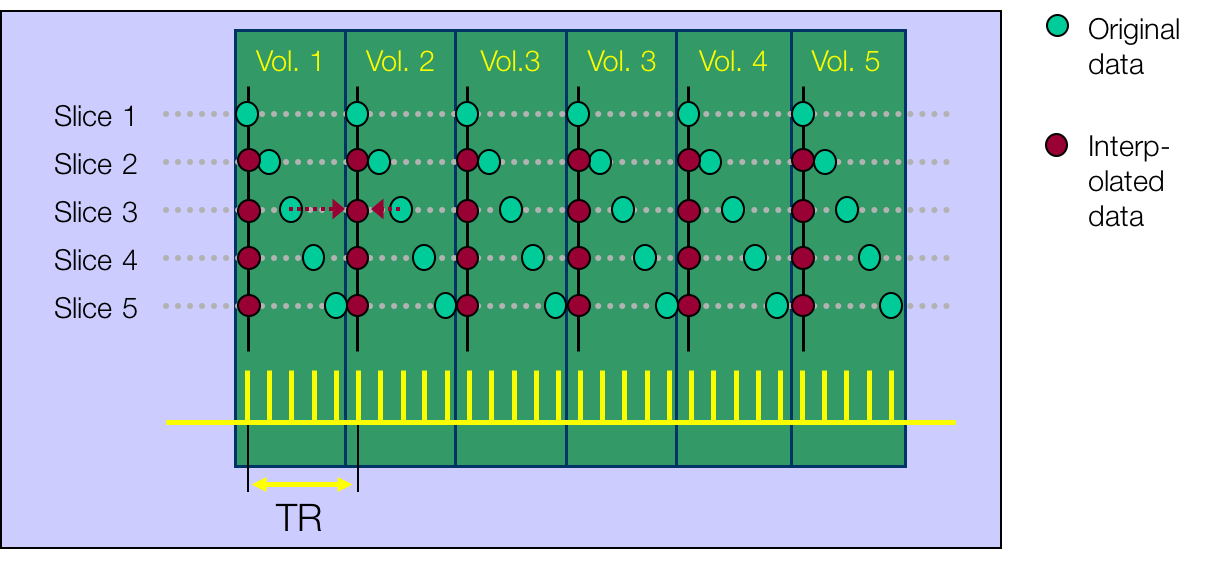
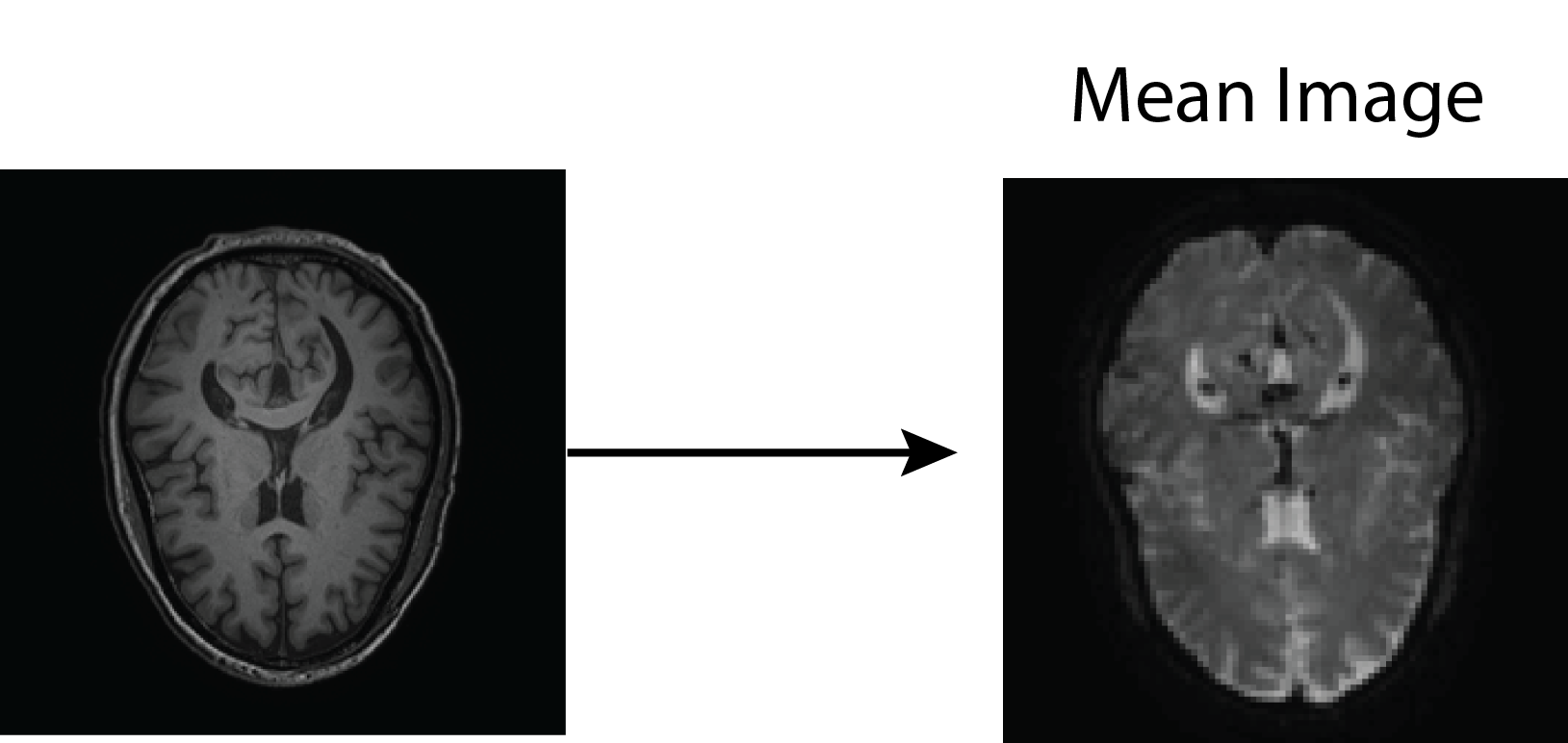
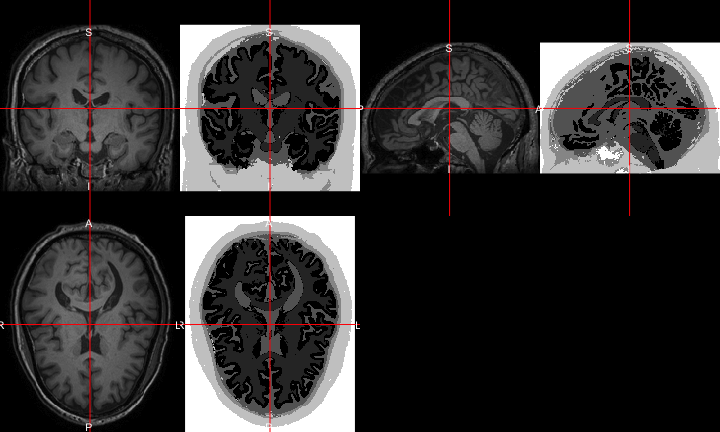
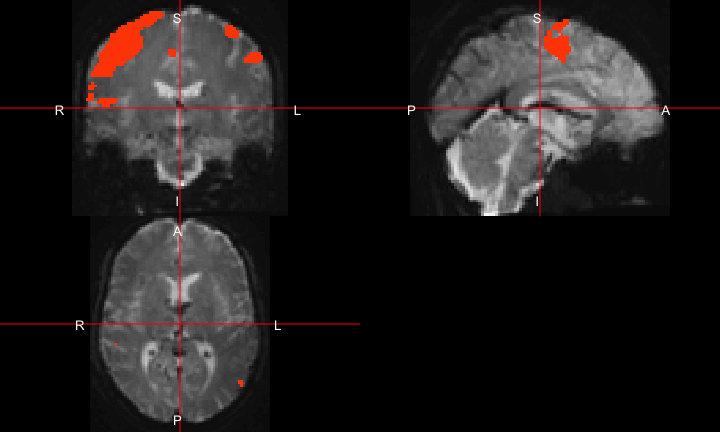
All of this is using the Statistical Parametric Mapping (SPM) (Penny et al. 2011) software version 12:
spm12r packagespm12r Worked Exampleanat.nii.gzfmri.nii.gz.dcm2niix (https://github.com/rordenlab/dcm2niix).dcm2niir: https://github.com/muschellij2/dcm2niirdivest: https://github.com/jonclayden/divesthttps://figshare.com/articles/SFO-example/5442298
url = paste0("https://ndownloader.figshare.com/articles/",
"5442298/versions/1")
# download a temporary zip file
zipfile = tempfile(fileext = ".zip")
res = httr::GET(url, write_disk(path = zipfile))
####### unzip file code (not shown) ###########
out_files = c("anat.nii.gz", "fmri.nii.gz")
fmri_filename = "fmri.nii.gz" tr = 1.8 # seconds hdr = neurobase::check_nifti_header(fmri_filename) # nifti header (nslices = oro.nifti::nsli(hdr))
[1] 60
(n_time_points = oro.nifti::ntim(hdr))
[1] 280
hdr
NIfTI-1 format Type : nifti Data Type : 16 (FLOAT32) Bits per Pixel : 32 Slice Code : 0 (Unknown) Intent Code : 0 (None) Qform Code : 1 (Scanner_Anat) Sform Code : 2 (Aligned_Anat) Dimension : 96 x 96 x 60 x 280 Pixel Dimension : 2.25 x 2.25 x 2.55 x 1.8 Voxel Units : mm Time Units : sec
The first part of any preprocessing pipeline should be to use exploratory techniques to investigate detect possible problems and artifacts.
fMRI data often contain transient spike artifacts and slow drift.
An exploratory technique such as principal components analysis (PCA) can be used.
(courtesy of Martin Lindquist)
Image taken from http://cnl.web.arizona.edu/imageprops.htm
For a voxel \(v\), the rigid transformation can be written as:
\[T_{\rm rigid}(v) = Rv + t\] where \(R =\) \[\left[\begin{array}{ccc} \cos\beta\cos\gamma& \cos\alpha\sin\gamma + \sin\alpha\sin\beta\cos\gamma & \sin\alpha\sin\gamma - \cos\alpha\sin\beta\cos\gamma \\ -\cos\beta\sin\gamma & \cos\alpha\cos\gamma - \sin\alpha\sin\beta\sin\gamma & \sin\alpha\cos\gamma + \cos\alpha\sin\beta\sin\gamma \\ \sin\beta & -\sin\alpha\cos\beta & \cos\alpha\cos\beta \end{array}\right]\]
realigned = spm12_realign(filename = fmri_filename, time_points = seq(n_time_points), quality = 0.98, separation = 3, register_to = "mean", est_interp = "bspline4", reslice_interp = "bspline4") # reading in the mean image mean_img = realigned[["mean"]] mean_nifti = readnii(mean_img) realigned$outfiles
[1] "rfmri.nii"
realigned$mat
[1] "fmri.mat"
(courtesy of Martin Lindquist)
slice_order = c(1740, 1680, 1620, 1560, 1500, 1440, 1380, 1320, 1260, 1200, 1140, 1080, 1020, 960, 900, 840, 780, 720, 660, 600, 540, 480, 420, 360, 300, 240, 180, 120, 60, 0, 1740, 1680, 1620, 1560, 1500, 1440, 1380, 1320, 1260, 1200, 1140, 1080, 1020, 960, 900, 840, 780, 720, 660, 600, 540, 480, 420, 360, 300, 240, 180, 120, 60, 0) ref_slice = 900 ta = 0 # since slice_order in ms
hdr)hdr)ref_slice),ta). ta = 0 if you give slice order in seconds/milliseconds.aimg = spm12_slice_timing(filename = realigned$outfiles, nslices = nslices, tr = tr, slice_order = slice_order, time_points = seq(n_time_points), ta = ta, # since slice order given in ms ref_slice = ref_slice, prefix = "a") print(aimg$outfile)
(courtesy of Martin Lindquist)
We then perform the coregistration of the mean image (fixed) and T1 (moving):
Coregistration is estimated using spm12_coregister_estimate:
t1_fname = "anat.nii.gz" coreg = spm12_coregister_estimate( fixed = mean_img, moving = t1_fname, cost_fun = "nmi") coreg$outfile
[1] "anat.nii"
spm12_coregister_estimate - estimates coregistration (transforms the header)spm12_coregister_reslice - reslices the image to the same voxel dimensions (should probably be coregistered already using estimate)spm12_coregister - estimates and reslices
Estimate the transformation, but do segmentation on native T1 space (better resolution)
Here we segment the image into 6 different regions, where the regions are gray matter, white matter, cerebrospinal fluid (CSF), bone, soft tissue, and the background.
seg = spm12_segment( filename = coreg$outfile, set_origin = FALSE, bias_corrected = TRUE, native = TRUE, unmodulated = TRUE, modulated = TRUE, affine = "mni", sampling_distance = 1.5)
native - native space segmentationsmodulated - adjusted segmentations to constrain tissue-class volumesunmodulated - unadjustedbias_corrected - save bias-field corrected imageset_origin - should AC/PC alignment be done (no because we just coregistered)
Affine + Non-linear transform (invertible)
The segmentation was done by warping the T1 to the MNI template and that transform/deformation in the segmentation output:
seg$deformation
[1] "y_anat.nii"
We apply the deformation to the fMRI data using spm12_normalize_write.
bounding_box = matrix(
c(-78, -112, -70,
78, 76, 85), nrow = 2,
byrow = TRUE) # change from default to reduce empty black space
norm = spm12_normalize_write(
deformation = seg$deformation,
other.files = aimg$outfile, #corrected fMRI
bounding_box = bounding_box,
interp = "bspline5")
anat_norm = spm12_normalize_write(deformation = seg$deformation, other.files = seg$bias_corrected, bounding_box = bounding_box, interp = "bspline5", voxel_size = c(1, 1, 1)) anat_norm$outfiles
[1] "wmanat.nii"
anat_norm2x2x2 = spm12_normalize_write( deformation = seg$deformation, other.files = seg$bias_corrected, bounding_box = bounding_box, interp = "bspline5", voxel_size = c(2, 2, 2)) # note the resolution!!!
Spatial smoothing should signal to noise depending on the size of activation
Typically, the amount of smoothing is chosen a priori
Usually global smoothing (same amount at each voxel), but can be adaptive (adimpro pacakge)
Specified using the full-width half max (FWHM) for the Gaussian smoother (not \(\sigma\)): \(FWHM = \sigma \sqrt{8 \log(2)}\)
smooth_norm = spm12_smooth( norm$outfiles[[1]], fwhm = 5, prefix = "s5")
In many applications, that smoothed data you will use for post-processing and analysis. Motion correction has usually been applied above, but some realign this again.
condition_list = list(
list(name = "LeftHand",
onset = c(20, 100, 180, 260, 340, 420),
duration = c(20, 20, 20, 20, 20, 20)
),
list(name = "RightHand",
onset = c(60, 140, 220, 300, 380, 460),
duration = c(20, 20, 20, 20, 20, 20)
)
)
regressor_mat - motion parameters and other “confounders” (not convolved with HRF)condition_list - conditions are convolvedfirst_model = spm12_first_level( scans = smooth_norm$outfiles, n_time_points = n_time_points, units = "secs", slice_timed = TRUE, tr = tr, condition_list = condition_list, regressor_mat = rpfile)
betas = list.files(pattern = "beta.*[.]nii"); print(betas)
[1] "beta_0001.nii" "beta_0002.nii" "beta_0003.nii" "beta_0004.nii" [5] "beta_0005.nii" "beta_0006.nii" "beta_0007.nii" "beta_0008.nii" [9] "beta_0009.nii"
SPM.mat - model specificationprint(first_model$spmmat)
[1] "SPM.mat"
weights indicate which coefficientscontrasts = list(
list(name = "LeftHand", weights = c(1, rep(0, 7)),
replicate = "none", type = "T" ),
list(name = "RightHand", weights = c(0, 1, rep(0, 6)),
replicate = "none", type = "T"),
list(name = "AllEffects",
weights = rbind(
c(1, rep(0, 7)),
c(0, 1, rep(0, 6))
), replicate = "none", type = "F") )
contrast_res = spm12_contrast_manager(spm = first_model$spmmat, delete_existing = TRUE, contrast_list = contrasts)
cons = list.files(pattern = "con.*[.]nii") print(cons)
[1] "con_0001.nii" "con_0002.nii"
stats = list.files(pattern = "spm(T|F).*[.]nii") print(stats)
[1] "spmF_0003.nii" "spmT_0001.nii" "spmT_0002.nii"
spmt = readnii("spmT_0001.nii")
ortho2(norm, spmt)
ortho2(norm, spmt > 5)
R pipelineR you’re goodPenny, William D, Karl J Friston, John T Ashburner, Stefan J Kiebel, and Thomas E Nichols. 2011. Statistical Parametric Mapping: The Analysis of Functional Brain Images. Academic press.